
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
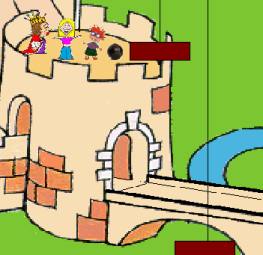 An elderly queen, her daughter, and little son, weighing
195, 105, and 90 pounds respectively, were kept prisoners at the top of a high tower. The only communication with
the ground was a cord passing over a pulley with a basket at each end, and so arranged that when one basket rested on the ground, the other was opposite the window. Naturally, if the
top one were more heavily loaded than the bottom, it would descend; but if the excess weight on either side was more than 15 pounds, the descent
became so rapid as to be dangerous. From the position of the rope, the captives could not slow it with their
hands. The only thing available to help them in the tower was a cannonball
weighing 75 pounds. They
nonetheless contrived to escape. How did they do it? An elderly queen, her daughter, and little son, weighing
195, 105, and 90 pounds respectively, were kept prisoners at the top of a high tower. The only communication with
the ground was a cord passing over a pulley with a basket at each end, and so arranged that when one basket rested on the ground, the other was opposite the window. Naturally, if the
top one were more heavily loaded than the bottom, it would descend; but if the excess weight on either side was more than 15 pounds, the descent
became so rapid as to be dangerous. From the position of the rope, the captives could not slow it with their
hands. The only thing available to help them in the tower was a cannonball
weighing 75 pounds. They
nonetheless contrived to escape. How did they do it?
Adapted from Merlin's Puzzle Pastimes, Charles Barry, Dover Publications.
Background & Techniques
Dover is a great publishing house for reasonably
priced books in many areas and with reasonable shipping cost.
If you get on their mailing list, they notify you weekly of a "Dover
Sampler" page where they reproduce a few pages from a dozen or so
books. This problem, from the $3.95 book, Merlin's Puzzle Pastimes, is on this week's sampler page.
When I decided to code this puzzle, I figured it would
be about an hour's exercise to do the fun part, the solution search. Six
hours later, the bare bones version was running. The hooker was realizing
that the extra move represented by the Cannonball traveling down alone is valid, even though it
violates the general rule about weight difference not exceeding 15 pounds.
Somewhere along the way, idea of animating the moves popped up,. so there went
the next 20 hours of spare time.
I think the problem would be fairly simple to solve without
computer help, but being able to drag and drop the prisoners (and the
cannonball) into the baskets and letting them move around does simplify
keeping track of things.
If you are not into "how things work", click
here to jump to the bottom of the page where you may download the executable
version of the program.
About the depth-first search algorithm
Here is how the "Solve" button works. It is a depth-first graph search useful for many simple games and puzzles.
- The first step in implementing a depth-first search is to decide how to identify positions in the game. In this case, I chose an
integer between 0 and 15. The binary representation of these numbers is a 4 digit number, each digit either 0 or 1. I arbitrarily assigned a
character to each position (Queen, Daughter, Son, Cannonball) and assign "1" to mean on top of the castle and "0" to mean on the ground.
So a key value of decimal 10 for example has binary representation of 1010,
which describes the condition with the Queen and Son up in the castle,
and the Daughter and the Cannonball on the ground. Think of these 16 keys as representing the nodes (corners, vertices) of a graph.
- Define the adjacency array. This is usually described as an adjacency list, but since we know there are only 16 nodes, a 16 X 16
array will do just fine. For each node, we need to identify all the other moves, nodes we could validly
reach by loading up
baskets and letting them move one time. We do
this by checking for each node which of the other 15 we could validly move to in a single basket trip. To be valid the weight represented by
the 1's (guys on top) must be greater than the weight represent by the 0's (guys on the bottom), but not more 15 lbs greater.
There is one exception to this, the Cannonball can always move from the top to the bottom by itself.
This means that any odd numbered node (Cannonball up) is adjacent to the
next lower even numbered node (Cannonball down). So for node N, we will fill in row N with
some positive number for the valid next nodes (I used the weight difference between the baskets) and negative number for the invalid
moves. In hindsight, a Boolean array would have worked just fine but at the
time, I thought that the weight differences might come in handy. They
didn't. Thinking of the graph analogy, this adjacency process defines the edges of the graph, the lines connecting the nodes.
Notice by the way, that these edges are directed, if we can get from node A
to node B, we can never get directly from node B back to node A.
Such a graph is called a "directed graph".
-
Now the game is to find a path on our graph from node 15 to node 1
(or 0) . Notice that for the starting node (1111, everyone up) the only valid move is to node 14
(1110, Cannonball moved down). From that node, row 14,
the only valid move is to node 13 (1101, Son down, Cannonball up). From node 13 we have three choices and things get interesting. We will
systematically follow the path through each node. Each step
will examine each node in the adjacency array for numbers greater than
zero. When one is found we add the move to Path, the list of
moves so far, mark the node as visited by setting the corresponding node as
true in the Visited Boolean array, and move to the next step using the next node
to visit. This is implemented in recursive procedure,
GetNextNode.
The first thing that GetNextNode does is to check to see if the node is a
solution (node number 1 or 0). If it is a solution , variable Solved
is set to True which will stop all additional searching. If we
reach a dead end, i.e. no more unvisited adjacent nodes, just take that move
out of the path, mark it as unvisited and exit back to the previous
iteration. This is the "backtracking" part of the
algorithm.
That's it for the search. The SolveBtnClick
method makes the initial call to GetNextNode with node number 15
and expects to return with the Solved flag set to true, If not, it
displays a "No solution found" message;
The other interesting programming challenge was the animation of the
moves. Given two nodes, "from" and "to", it's a
bit tricky determine exactly what has changed. It turns out
that the "XOR", exclusive or operation is just the ticket.
XOR'ing the two nodes will produce a number with 1's for the items that
were in the basket and 0's for those that stayed put. It
is also necessary to determine which direction the item moved and which basket
they were in. In hindsight, it would have been cleaner to make
"item" and "basket" objects and let them keep track of where
they were and all their other properties. By the time I realized this, I
was too lazy to start over. We'll put that suggestion down in the
"Suggestions" section. Two
animation "tricks" come to mind. To improve the images, I made their
backgrounds transparent. Do do this, character images must be loaded
as bitmaps, then turn on the Transparency property in Timage and set the transparency
color in Picture.Bitmap to clwhite (or whatever color your
backgrounds are).. The second trick
was to set the Doublebuffered property to true for the Tabsheet
that contains the images in order to eliminate flicker while the animation is in
progress. .
Running/Exploring the Program
Suggestions for Further Explorations
 |
As
suggested above, code would be simplified by creating TItem and TBasket
objects derived from TImage controls. They would know
where they were, names, weights, their picture, etc. |
 |
The
weight of the people and the cannonball could be user input values,
allowing other problems to be posed. |
 |
The
animation is a little slow on my 400mhz Celeron system. I can't
recall that I've ever done it, but it should be possible to detect CPU
speed and adjust the animation accordingly. |
 |
The
drag drop processing for user play is as simple as I could make it.
More work could display each character as it is being dragged, but
you need "can drop here" and "can't drop here"
versions of the image - kind of a pain. |
|
Created:
August 9, 2003 |
Modified:
May 15, 2018
|
|

