Problem Description
 Here's a Delphi version of a classic Water Jug
problem. One version goes like this:
Here's a Delphi version of a classic Water Jug
problem. One version goes like this:
Two
friends who have an eight-quart jug of water wish to share it evenly. They
also have two empty jars, one holding five quarts, the other three. How
can they each measure exactly 4 quarts of water?
(Solution takes 7 pour
operations.)
Background & Techniques
Viewer Charles Doumar wrote the original program and introduced me to
the Water Jug problem as a test of our TGraphSearch unit which
incorporates the Dijkstra Shortest Path Search algorithm. Alex
Bogomolny's Cut the Knot site has a good Water
Jug problem page some of the history and theory.
Because this version is designed as a test of shortest path searching,
we allow any combination of starting values with any other
achievable combination as a goal. The solver initially knows
the capacity and amount of liquid contained in each jug and is searching
for a given goal configuration. The jugs have no intermediate
measure of the amount contained so pouring transfers the smaller of
(1.) the
amount of water in the "From" jug and (2.) the available unused
capacity of the "To" jug. And, of course, the fewer moves
the better.
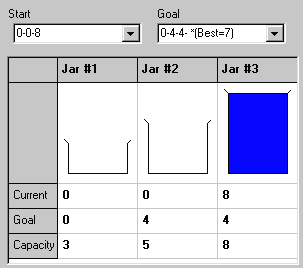
Users may set up any 3 or 4 jug puzzle and try to solve it by clicking
on jug images. When you're ready to give up, as I
frequently am, the "Show me" button will compute the necessary
moves.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to
download the executable version of the program.
Programmer's Notes
The program uses procedure Dijkstra from
the TGraphSearch class to search for solutions.
At the top of the form the user selects the number of jugs, 3 or 4, the
capacity for each jug and the total amount of water to be distributed
across the jugs.
When any of these amounts change, a call to JarBtnClick
generates nodes for all possible ways to distribute the specified
water amount across the available jugs. The TComboset
Combos class is then used to generate all pairs of jugs from
the available number. If the first of the pair could pour an amount
>0 into the 2nd of the pair, a graph edge is generated connecting the
two.
Once the nodes and edges have been built, TComboboxes,
StartCB and EndCb, are loaded with the available nodes
from which the user will select starting and ending jar configurations. When
the start configuration is changed in StartCB, an attempt is made to
evaluate the result for all goal nodes in EndCB. For four jar cases
with large capacities, this process might take a long time, so a "Stop"
button is provided to abort the process. The results of the solution
search are used to pre-calculate "Unsolvable" goals which are
flagged in the end goal text and "best solution" move counts,
which are retained as objects with each goal entry and displayed when the
"Show best solutions" checkbox is checked. The best
goal count is also used to modify the message given when a solution is
found manually ("Congratulations!" or "Good,
but it can be solved in fewer moves")
User play is controlled by an OnDrawCell exit in
a TStringGrid which draws scaled images of the jugs (they look more like
beakers, but oh well). Users click on the images define from
and to jugs and the move is displayed in a Tmemo display area.
Whew! 700 lines of code is enough to put
the program in the Advanced category.
Addendum: February 18, 2010: A 7
jug problem sent by a viewer led to a major rewrite of this program over
the last month. Version 3 solves cases much faster than the
earlier version and handles problems up to 7 jugs in size.
Melanie's 7 jug problem is displayed as the default for that size and
takes a couple of minutes to find the shortest solution which requires
48 moves! Most other cases I've tried find the solution in under a
second. Internally, Dijkstra and the Graphlist are longer
used. That method required building the complete search state
graph before running the search. For large cases this is not
feasible. The search now is a breadth first search for the goal
configuration but generating only those goal states which derive from
the starting configuration. There were some interesting problems
to solve in removing the recursive search procedure used in the
prior version. See the source code or write if you are interested
in the details.
Addendum: April 21, 2010: A second type
of Water Jug puzzle, which I am calling "Open" puzzles, was introduced
today with Version 4. The original puzzles implemented here are
"Closed" in the sense that water may neither be added or subtracted from
the initial amounts while solving. "Open" puzzles allow water to
be added or subtracted by filling or emptying any jug in addition to
pouring from one to another. Searching "Water jug puzzles" on the
web will return a number of problems of this type, including a classic
one from a "Die Hard" movie in which 4 gallons of water must be obtained
when only jars with capacities or 3 and 5 gallons are available.
Running/Exploring the Program

