
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
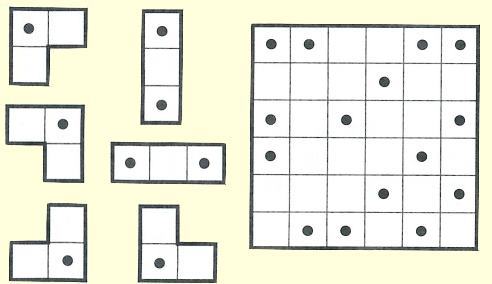
One or more copies of the 6 given shapes have been used to tile the grid and then the
outlines were removed. Can you fill them in again?
Background & Techniques
The 6x6 grid at right was tiled using only the two "tromino" shapes and their
rotations. (Four orientations for the "L" shape and two for the "I"). Use as
many of each tromino as needed. The locations of the tromino dots are shown on
the grid but without the outlines.
This initial version of the program does not support user play, so, for now,
you'll have to print or copy this screen to work on solving the puzzle for
yourself.
The Search button on the program form animates the program solving the puzzle by
"trial
and error". Tiles are placed from left to right and top to bottom, trying all
six tile versions in succession and backtracking when we reach a dead end. I've
inserted a 1 second delay after each placement or retraction so you will be able
to follow the process. By coincidence there is only one location near the bottom
of the grid
where the first tromino which can be placed is not the correct one and the
program must backtrack and replace it a few steps later.
Source: "Mensa "Puzzle Calendar" for May 5, 2014.
Non-programmers are welcome to read on, but may want to jump to bottom of
this page to download the executable program now.
Programmer's Notes:
An early step any program development project is determining the data
structures which will model the puzzle elements. For a puzzle or game
which is played on a 2 dimensional board or grid, I routinely let a TStringGrid
control represent it. StringGrid cells contain string data but can also
have more complex objects associated with the via the Objects property. In
this case, I chose a string structure to represent tromino and cell
contents. Trominoes are 2x2 string arrays for the four 'L'
trominoes, and 1x3 and 3x1 arrays for the 'I' trominoes. Grid and tromino
cells strings are 6 characters in length defined as follows:
| Position |
Contents, |
| 1 |
' ' = Display blank, 'D' = display a centered dot , (For a
tromino definition '_' = unused corner of the 2x2 tromino.
|
| 2 |
'0' = cell unassigned, '1' through '6' = contains a cell of
tromino type 1 through 6 |
| 3 |
'1' = draw top edge, '0' no top edge |
| 4 |
'1' = draw right edge, '0' no right edge |
| 5 |
'1' = draw bottom edge, '0' no bottom edge |
| 6 |
'1' = draw left edge, '0' no left edge |
"Recursive Search with Backtracking" is a systematic search technique
which takes advantage of the fact that placing a piece on the board is pretty
much the same for each piece placed. In this case, function
PlacePiece(x,y) looks for one of the six tromino shapes that will fit with
its top left corner in the empty grid cell at column x and row y.
PlacePiece calls function Fits(x,y,i) which does the checking and
returns "True" if tromino it fits at (x, y). If Fit
returns True then procedure Place is called to actually fill in
the grid cells with the tromino definition strings. PlacePiece then finds
the next unfilled cell and calls itself with with that top-left coordinate.
If PlacePiece tries all 6 trominoes and cannot find one that fits, it
return false to the previous PlacePiece caller location which will
the call Remove procedure to undo the piece he added and continue
searching for another choice. This is the "backtracking" side of
"recursive search with backtracking". If PlacePiece runs out of
empty cells to fill, the puzzle is solved. I returns True to the calling
level which passes back up the line until answer comes back to the initial call
made from the SearchBtnClick procedure.
There were a couple of new complications in implementing the above.
 | The search for open grid location by moving left to right and top to
bottom works well except for the reversed L tromino where the first
empty cell is top-right corner rather than the top-left corner.
PlacePiece detects this condition and passes the prior column to Fits
function when top-left tromino cell is unused. |
 | Placed trominoes are outlined inside of cell boundaries in a DrawCell
StringGrid exit. This leaves corners unconnected drawn unless special
actions are taken. First fix was to draw extend connecting lines back
into the adjacent cell by W, the "wall offset" distance. This worked
in almost all corners except when the extended border line is overwritten
when that cell is drawn. A couple of exception statements handle the
two cases and replace the previously drawn line extensions.
|
All-in-all, this was a good medium complexity project requiring about 500
lines of code and a week of spare time programming fun.
Running/Exploring the Program
Suggestions for Further Explorations
 |
Add user play |
 |
. |
| |
|
| Original: May 14, 2014 |
Modified:
May 15, 2018
|
|

