
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
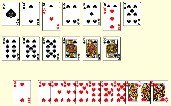 Here's
a simple puzzle that can be solved with or without a computer. Remove
the 13 spades and 13 hearts from a deck of cards. Layout the 13 spades
and place the 13 hearts, one on each spade so that the sum of each pair of
cards is a perfect square (1, 4, 9, 16, etc.) for every pair.
Jacks, Queens and Kings have values of 11, 12 and 13 respectively. By the way, don't count on the start shown
here being correct. Here's
a simple puzzle that can be solved with or without a computer. Remove
the 13 spades and 13 hearts from a deck of cards. Layout the 13 spades
and place the 13 hearts, one on each spade so that the sum of each pair of
cards is a perfect square (1, 4, 9, 16, etc.) for every pair.
Jacks, Queens and Kings have values of 11, 12 and 13 respectively. By the way, don't count on the start shown
here being correct.
Background & Techniques
This was a fun one day project mainly to see if the
card drawing unit introduced last year still works (it does). I added a
hint button that will help anyone that gets really stuck. (Only partial
credit if you solve it with hints though.)
I ran across this problem description in Martin
Gardner's book: "Time Travel and Other Mathematical
Bewilderments" , Freeman Books, 1988. The problem is
attributed to David L. Silverman.
Non-programmers are welcome to read on, but may want
to skip to the bottom of this page to download an
executable version of the program.
Notes for Programmers
The structure for this problem is pretty simple. Array Board
is an array of 13 integers. the position of each number in the array
represents the Spade value and the value of each entry represents the Heart
value. So for each filled entry, i+board[i] is a square
number. An IsSquare function checks whether a passed value is
a square.
The code has two main functions:
 | Manage card objects as the user drags them around: I use the U_CardsComponent introduced in Cards
2 to define the 26 cards needed. The global array, Board,
holds the current status of the cards. We'll use the FormDragDrop
procedure to do the necessary checking and updating the Board
array. At drop time we also check to see if all cards are in
place.
|
 | Deliver hints to user on request: A recursive function, GetNextMove, is called at FormCreate
time to build a TargetBoard array with the final positions of the
Hearts. This, together with the Board array, lets us decide which card should be moved temporarily to its proper location
when the user clicks the Hint button. .
The MoveCard function cleverly adjusts the pixel increment to
maintain a reasonable move speed across processors of differing speeds
while displaying hints. If the card moved faster than 250 pixels per second,
the increment is decreased; if slower the increment is increased. |
Running/Exploring the Program
Suggestions for Further Explorations
 |
Probably not
much more for this problem. But there are hundreds of others just
waiting in the wings. Here's one more example from Gardner's Time
Travel book:
- Place the 13 cards of any one suit face up in a row,
Ace through King
- Starting with the 1st card, turn over every card
- Starting with the 2nd card, turn over every 2nd card
- Start with the 3rd card, turn over every 3rd card
- Continue in manner until, on the 13th pass, you turn over only
the 13th card.
Which cards are face up? Can you figure out why? |
| Original Date: July 14, 2002 |
Modified: May 15, 2018
|
|
|
|

