
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
This program implements a board game called Paletto and a puzzle derived from
it.
Background & Techniques
Paletto is a game for 2 to 4 players designed by Dieter Stein and described
on his website
http://spielstein.com/games/paletto. The rules are simple and play is easy
but some strategic thinking is required to win. The physical game is
manufactured and marketed by Clemens Gerhards on eBay and, along with many other
attractive games, on his website
http://www.spiel-und-design.eu/en. The games look to be of excellent
construction and reasonably priced at around $25. Unfortunately, shipping to the
US adds $48 to that price making unlikely that I will ever own one!
 |
| Partial game: The 3 Purple tiles
might be a good choice for Player 1 |
The Game
The physical game is played on a 6x6 board and has 6 balls of 6 different
colors, 36 in all. A game starts with all of the balls randomly placed on
the board. In serious competition, a third party would have to load the board
since it would be easy for a knowledgeable player to "stack the deck".
Players take turns removing eligible balls of a single color. The game is
won by the player who either takes all pieces of any color or whoever takes the
last piece from the board. Players take turns. In each turn a player chooses a
color, then removes any number of same-colored pieces (not necessarily all) from
the board by clicking on them.
A piece may be removed from the board if:
 | There are two or more open sides (board edges or touching an empty cell)
and |
 | All remaining pieces after the move are still "orthogonally
connected", that is, one could travel from any occupied cell to any other
occupied cell by making horizontal and vertical moves. |
The puzzle described below requires an 8x8 board so and 8x8 version of the
game has also been implemented.,
 |
|
First 3 rows while solving |
The Puzzle
I became aware of the game because a long time viewer and fellow Delphian
residing in Germany owns
the game and had developed a puzzle idea based on it but wasn't sure that it was
solvable. After a few
iterations, we proved that it is solvable and is included here as "Puzzle 2",
both as a user playable version and
the solution search that proved it could be done. For the puzzle, we are required to fill an 8x8 board with 64 balls or
tiles, 8 balls in each of 8 colors following 2 rules.
 | Each tile and its the vertical and horizontal neighbors, if any,
must be of different colors (requiring 5 colors for interiors tiles).
|
 | Each corner of the board must be of a different color. |
Users play using "click-drag" operations. Click a tile from the 8 tile
"piles" which pick it up, move to the target cell and click again to drop it.
A "beep" indicates that the attempted placement is invalid. Tiles in place
may be clicked and returned to the available stack or dropped on any other empty
cell on the board.
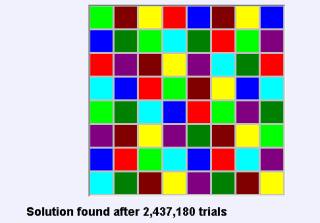 |
| Random program search solution |
The programmed search to fill the board performs a trial and error
search to find a tile which can be placed without violating the rules, If none
can be found, the program "backtracks" to the previously placed tile and tries
to find another valid choice. Options allow the board to display color numbers
(1 through 8) or colored tile in either the order that they were defined or in
random order. There is a "Show progress" box to watch the backtracking
process. For random board solution, the amount of backtracking required
depends on how the early tiles got placed. Typically between 4,000 and
4,000,000 tile placements are required before a solution is found.
Non-programmers are welcome to read on, but may want to jump to bottom of
this page to download the executable program now.
Programmer's Notes:
Program logic is a quite straightforward implementation of the rules.
However there are a few interesting techniques used (or reused) here:
 | "Click dragging", dragging without holding a button down:
Especially when using a touchpad to drag across a grid, it is easy to
accidentally drop the object in the wrong place. A simple solution is
to define a flag to indicate when dragging is taking place. Here we
use an integer variable, DragColor, to indicate both that a tile is
being dragged (DragColor>0) and the color index of the tile color
being dragged. A second MouseUp on at an eligible location when
Dragcolor >0 marks the "drop" operation.
|
 | Creating a colored square as a "drag" cursor for each color during
manual play of the puzzle: The process is straightforward using the
TIconInfo data structure to hold the bitmap (a colored square in this
case) and the CreateIconIndirect Windows API call to assign the
cursor to the array of Screen cursors. This is done in the
FormActivate procedure for all 8 colors. |
 | To recognize where a mouse click is made on a string grid: The
MouseToCell method of TStringGrid handles this nicely. The
OnMouseUp event exit will return the X and Y mouse coordinates more
readily than using the OnClick exit. |
 | Moving the mouse cursor to a specific grid cell: This inverse
problem occurs here when the user is dropping a tile back onto the
tile stock pile grid when manually solving the puzzle.
Dragcolor is the color number of the tile being dropped with values 1
through 8, corresponding to columns 0 through 7 and we want to recognize any
click on the stock pile grid while dragging as a signal to drop the tile on
the cell from whence it came. Here's the code:
 | acol:=dragcolor-1;
r:=StockPileGrid.CellRect(acol,1);
{the rectangle containing the color}
{move the mouse cursor to the center of this
rectangle}
with r do mouse.cursorpos:=ClientToScreen(point((left+right)
div 2, (top+bottom) div 2)); |
|
 | Shuffling the color array to control the order of trying colors for
random solutions: Procedure Shuffle randomly rearranges any
array of integers by swapping each number location, starting at the high end
of the array, with a random location less than or equal to the current one. |
 | Manual vs. program checking in solving the puzzle: There are two sets of
offsets; the programmed search proceeds from left to right and top to bottom
and therefore only needs the verify that the tile being placed does not
match either of the two preceding neighbors to the left of or the two above the
current location (4 tests in all). The human player however may place tiles in any
order and therefore we must check 2 neighbors in each orthogonal
direction as well as the 4 diagonals, 12 tests in all to ensure that
the tile may be safely placed.
|
 | Recursive Placepiece function places pieces and retracts and
tries a different color for the previous move when no valid color exists for
the cell being filled: Long time DFF followers will recognize the
"recursive search with backtracking" exhaustive search technique
used in many programs here for puzzles which require no more than a
few million trials. When the "Show progress" box is unchecked, the search
process about 1,000,000 locations per second and solves most cases in a few seconds.
Watching the progress slows the process down significantly. |
Addendum February 4, 2013: I received a note today from
Paletto's author, Dieter Stein. He likes the program but pointed that the
initial board for the game must not share a side with another token of the same
color which I did not realize. This restriction prevents the person
placing the tokens initially from "stacking the deck" as I had initially
mentioned. Version 2.1 posted today corrects the problem by generating
random boards until a valid one is found. About 1,000,000 boards per
second can be created and tested. Making new 8x8 boards may take a few
seconds (up to 5,000,000, tries) but 6x6 boards require only a few hundred
thousand trial boards, so appear almost instantly.
Running/Exploring the Program
Suggestions for Further Explorations
 |
Teach the program to play the game against a
human opponent, |
| |
|
| Original: January 17, 2013 |
Modified:
May 15, 2018
|
|

