

[Home] [Puzzles & Projects] [Delphi Techniques] [Math topics] [Library] [Utilities]
|
[Home] [Puzzles & Projects] [Delphi Techniques] [Math topics] [Library] [Utilities]
|
|
|
| Two players. | |
| It is a sequential game - players take turns moving. | |
| The game state can be represented by a board containing all the pertinent information. | |
| Both players have knowledge of of all possible next moves. This is called a perfect knowledge game. This excludes card games with hidden hands, for example, since we do not know all of our opponent's play choices. | |
| Game moves are not random - this usually excludes games involving dice or spinning dials. | |
| The games are finite - they all reach some terminal configuration representing a win, loss or draw result. |
The initial game board is the root node of the tree. The children of any node are the board positions that can be reached in a single move. Each branch of the tree terminates in a leaf node which has no further moves and represents a win for one of the players or a draw.
Nim, Tic-Tac-Toe, Checkers, Go, and Chess are typical games suitable for game tree representation. Here's a portion of the game tree for Tic-Tac-Toe (lifted without permission from a gamasutra.com page)
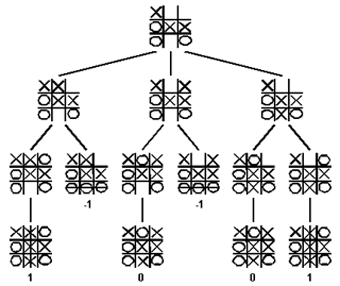 |
In this diagram "X" winning positions give a value of 1, "O" winning positions are given value -1 and ties have value 0. We'll see why in a few minutes.
One more item before we move on. Call the player who moves first Player A, and the other player, Player B. If we assign a level number of 1 to the root node and increment level numbers for a node's children that by 1, then Player A's moves will be from an odd numbered levels and Player B's will be from even numbered levels.
Minimax is a search method for game trees that provides guidance for good play. The minimax algorithm assigns values to game tree nodes. Higher values represent higher probabilities of winning for Player A. This also means that higher values reflect smaller probabilities of a win for B. Conversely small numbers reflect small probabilities of A winning and high probabilities for B winning. When examining a Player A node that has children, the value assigned is the maximum of its children's values. When it is Player B's turn, we assume that he will choose the move which is optimum for him. This is also worst choice for Player A. That is, B will choose the child node with minimum value as his next move. Applying this algorithm recursively, we can determine the optimum move for either player from any starting board popsition.
Assigning the lowest level node values could be the trickiest part of implementing minimax. For simple games like Nim and Tic-Tac-Toe, we can afford to analyze the entire game tree and assign payoff values only for the terminal (leaf) nodes. This simplifies things considerably. We'll assign a value of +1 if the node represents a winning position for Player A (i.e. it's at an even level) and -1 if it is a winning position for Player B (an odd level). For Tic-Tac-Toe, it is common to assign values of +1, 0, -1 for Player A win, draw, and lose respectively. The game tree for Chess is estimated to have more than 10100 nodes, impossibly large, so Chess playing programs typically search a few levels down, using a payoff function to evaluate the goodness of future positions furthest down the chain. The minimax technique is then applied to these values as if they were leaf nodes. Not perfect, but more practical than spending 1080 years to find the perfect move.
If any non-programmers made it this far, you may want to jump to the download section now.
Let me remind beginners, that even though it may seem that these programs spring full blown from the fingers of a genius, that's far from the truth. The 200 or so lines of code in this program do not reveal that many lines lie on the cutting room floor. This is the third fairly complete Nim rewrite. For example, early attempts retained child nodes as part of the node structure, and tried to build an actual tree structure - for no good reason as it turned out. Terminal nodes were initially identified as a position with a single remaining stick. That's OK unless someone deliberately loses by take the last two sticks in no move. Ooops, the 1 remaining stick node never exists. Just two of many initial false starts.
The final version uses a simplified TNode with only 3 variables object to define the game position:
| Sticks - the number of sticks remaining. | |
| Level -number of levels deep into the tree, starting from level 1 for the root node). | |
| HighChildIndex - the number of sticks to take to get to the child with optimum value. This is the number of the child with maximum value for Player A and the number of the child with minimum value for Player B. |
Function Search is the critical routine in this program. Pass it a node and it will return the node's value and also fills in HighChildIndex in the node. It accomplishes this by generating nodes for each of the valid children (nodes with 1, 2, and 3 sticks removed), recursively calling Search with each child and finding the maximum (for odd levels) or minimum (for even levels) values of the children. If there are zero sticks remaining in the node passed, there are no valid children and this is a terminal node. The value for a terminal node is +1 if it is Player A's turn (It's A's turn and there are no sticks left, so B must have taken the last one, so A wins), and, conversely, -1 if it is Player B's turn.
CurrentNode is a global node variable that keeps track of where we are in the game.
I decided to write Nim as a human vs. human game with a Suggest button to run the minimax search and suggest the best move for the current player. This just saves a radio box to choose whether the computer has the role of player A, B, neither or both. The node variable HighChildIndex set by Search is only used by the top level call from the SuggestBtnClick exit. It's used to report the best move back to the user.
DrawBoard is a procedure that draws a simple image of the sticks remaining. The image may be overlaid by by a DebugBox listbox containing debugging messages from search routine. DebugBox is normally invisible, unless a condition compiler symbol DEBUG is defined. The conditional compiler directive IfDef is used to control whether or not debugging code is generated.
| Browse source extract | |
| Download source | |
| Download executable |
There are many places to go from this starting point:
| Here's a link to an excellent page from a 1997 McGill University Computer Science class; Data Structures and Algorithms, Topic #11, Game trees and Alpha-Beta Search | |
| There are reversed versions of many two-person games, called miseré games for some reason. (My dictionaries say that the word means "misery" in German or French.) In any event, in this "reversed" version of Nim, you win by taking the last stick. It should be a fairly simple enhancement to allow the user to select "normal" or "reversed" versions of play. | |
| Additional games - I believe that I'll tackle Connect-4, a four-in-a-row game similar to tic-tac-toe. There are also more complex versions of NIM with multiple piles of sticks but I can't recall the details. | |
| Partial evaluation - it would be fun t tackle a game complex enough that complete tree evaluation is not feasible. | |
| Alpha-Beta pruning is a minimax search modification that speeds of solution searching by truncating searches when they cannot possibly lead to the best solution. For example, assume were in Node N looking for a maximum and child C1 returns a value of 10. We know therefore that the final value of N will be greater than or equal to (>=) 10. Now consider the evaluation of child C2 - remember that since N is at a maximum level, it's children including C2 are at a minimum level - final value of C2 will be the minimum of the values of all of its children. So if C2's first child happened to return a level less than 10, say 9, we know that the final value of C2 will be less than or equal to (<=) 9, even if there were 100 more children that we haven't examined yet. Since the final value of C2 will be <=9, it cannot affect the final value of N (we already know that N will be >=10). We can thus "prune" the search and not even bother to evaluate any additional children of C2; saving all those CPU cycles for more important work. Whew! This is a case where a picture would be worth 1000 words, so visit the McGill University link mentioned above if you want more information. |
Modified: May 15, 2018
[Feedback] [Newsletters (subscribe/view)] [About me]Copyright © 2000-2018, Gary Darby All rights reserved. |