Problem Description
 Fill in the numbers 1 through 27 in the
cube layers at left so that the sum of the
following 31 sets of 3 numbers each are
all identical:
Fill in the numbers 1 through 27 in the
cube layers at left so that the sum of the
following 31 sets of 3 numbers each are
all identical:
-
Sum of each row within each layer, (9 sums)
-
Sum of each column within each layer, (9 sums)
-
Sum of each vertical column across
layers, (9 sums)
-
Sum of each diagonal connecting the 8 corners of
the cube (4 sums).
Background & Techniques
 Magic cubes are one of many
interesting detours in the study of magic squares.
Recall that magic squares are N x N arrays of numbers containing the
numbers 1 through N2 with the property that the sum of the
numbers in each row, column and diagonal have the same value.
Magic cubes are one of many
interesting detours in the study of magic squares.
Recall that magic squares are N x N arrays of numbers containing the
numbers 1 through N2 with the property that the sum of the
numbers in each row, column and diagonal have the same value.
Magic Cubes extend this idea to three
dimensions. Unfortunately, magic cubes below order 6, have a
defect; we can't get the diagonals on the 6 cube faces to add to
the magic number. For lower order cubes, we can however build examples
that have identical sums for all of the rows, columns and pillars as well
as the four diagonals that connect the 8 corners of
the cube .(sometimes called triagonals). Such cubes are called
semi-perfect magic cubes. Here's a program that generates all
192 solutions
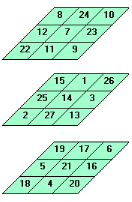
for 3 x 3 x 3 cubes. Of the 192 solutions, only four
are unique. The rest are rotations and reflections of these four. (48 per
solution).
Much of the information on this page came from the Internet and
from a chapter in Martin Gardner's book "Time travel and
other mathematical bewilderments", Freeman, 1987.
Non-programmers are welcome to read on, but may want to skip to the
bottom of the page to download an executable version of the
program.
Notes for programmers
The program is a fairly straightforward implementation of a brute-force
exhaustive search for solutions. I'm pretty sure
that here are more efficient methods, but it is comfortable to work
from first principles. This program does, but it will run an
hour or so to find all solutions. Higher order cubes would certainly
require a more efficient algorithm.
The magic constant representing the sum of each column, row or pillar
for a cube with N3 elements is (N3+1)×N÷2.
You can derive this for yourself by recalling that the sum of all of the
numbers in the cube is the average number, (1+N3)÷2,
times the number of numbers, N3, giving the
expression (1+N3)×N3÷2. This
number must be divided evenly across the N layers giving the sum for each
layer and be divided by N again to get the sum for each row or column in
the layer. In our order 3 case, (27+1)×3÷2
= 42.
So we start by examining all sets of 3 numbers selected from 1..27 and
saving those that sum to 42. There turn out to be 85 of these
triples, ignoring order. Each of these sets of three number can be
rearranged in 6 different ways, and we'll generate the 6 permutations of each
triple as we test them for inclusion in layers.
Next we'll select all possible layers of the cube, a layer is a
set of three of these triples that form a square and meet the
criteria that no duplicate numbers are included and the sums of the three
1st members of the triples, the three 2nd members and the three 3rd
members all sum to the magic number. There are nearly
71,000 of these!
Once these are generated, we can start the search for three layers
meeting the final criteria to make our magic cube. Due to the length
of the search, I implemented an automatic
save/restore procedure to allow interrupted searches to resume.
Solutions are saved to a file named MagicCube.strm and automatically
restored at startup time.
In order to speed testing, I decided to generate keys for each triple
and for each layer that contained 1 bits for each number that was
present. Since we have only 27 possible numbers and 32 bits in
a integer type field, there is plenty of room to do this. We
will count from the left so the key for, say 6, would be generated as
1 shl 5 (1 shifted left 5 times) = 32. The mask
for N is generated as 1 shl (N-1). We
can OR these mask values for each number with a key being constructed. The end
result is an integer that has bits turned on for each number in the
triple or layer. Two of these keys ANDed together will
produce a result of 0 of the structures represented have no numbers
in common, or non-zero if they have elements in
common.
This same key generation technique is used when determining whether a
particular cube is unique or some transformation (rotation or reflection)
of one already found. The trick here was to recognize that the cube
corners are preserved across rotations and reflections. So if we
build keys from the 8 cube corners, any two with the same key
will be rotations or reflections of each other. (This
would not be the case for higher order cubes though.)
The simulated 3D drawing of the cube layers was another interesting exercise that
took several hours of play to develop. Not very elegant,
but it seems to work fairly well.
Enough chit-chat, lets get to the program.

