[Home]   [Puzzles & Projects]    [Delphi Techniques]   [Math topics]   [Library]   [Utilities]

Problem Description

Drag the lettered blocks onto the template to form valid words reading across and down crossword style.  No need to rotate pieces and each piece is used exactly once.  Here's what the downloaded puzzle looks like:

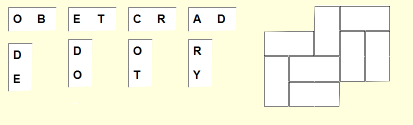
Background & Techniques

The puzzle is the first and only example of this type I've found in my many years as a fan of the Mensa "Puzzle-A-Day" calendars.  It's from the June 18, 2010 puzzle page.

To play, drag and drop blocks onto the template, horizontal blocks onto horizontal spaces and vertical blocks onto vertical spaces. To replace a block drag the incorrect block anywhere off of the template.  Use the "Hint" button for a littler help if you get stuck.

A future version will add dictionary lookup capabilities so that many additional valid puzzles can be generated (I hope!).

Non-programmers are welcome to read on, but may want to jump to bottom of this page to download the executable program now.

Programmer's Notes:

Job 1 for implementing a computer model of a real world object (this puzzle, for example), is to determine the data structures which will let us  describe and manipulate the parts.   In this case, TStringGrid controls are logical candidates for the lettered blocks and the board template which controls where the blocks can be placed.    Using Delphi's ability to define new classes, I defined a TBlock class as a TStringGrid descendent with a few additional fields.  Namely

There's an array, Block, of TBlock controls defining the 8 blocks.  Each block gets a lot of information from 8 TStringGrid controls that I defined using Delphi's visual design capabilities.  See TBlock.Create and TBlock.Assign for the details.  This allows us to reference any of the blocks using  common code referencing Block[i].   Setting the Dragmode property to dmAutomatic allows the blocks to be dragged using the mouse.  The board . template, named Board, is a 5 x 4 TStringGrid which has OnDragOver and OnDragDrop exits to allow properly oriented block to be dropped on it. 

In order to identify where the blocks can land and where they should be when the puzzle is solved I defined a 3-dimensional BlockMap array [0..4, 0..3, 0..1]  containing two integer values for each of the 5 columns and 4 rows of the template grid.  The first digit is simply an index number assigned to each block target location, '0' to '3' for the horizontal blocks and '4' to '7' for the vertical blocks.  The four top left and bottom right cells are assigned a value of '-1  to indicate that no block can be dropped there.  The second digit for each cell contains an offset value of '0' for the  top left cell of each block and '-1' for the other cell for each block.  This way, when the user drops a block on the board, the drop cell plus the offset value will point us to the first cell of the block.    Here's how BlockMap identifies the block locations:

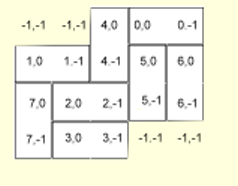
How do we use Blockmap? 

1. The OnDrawCell exit for the Board get passed a column and row to draw each cell where we want to draw an outline of the the left or right end of a horizontal block or the top or bottom for a vertical block.  The exit uses the BlockMap data to determine how to outline that cell. 
2. When the user drags a block over the board, an OnDragOver exit must set an "Accept"  Boolean variable to true or false to control whether the block can be dropped at that location.  BlockMap provides it with the necessary information.
3. When the user drops the block on an acceptable location, we move the top left corner of the block to the top left corner of the template location.  The first BlockMap value for the drop cell tells us whether it is a horizontal or vertical block (<=3 for horizontal) and adding the second index value to the column (for horizontal blocks) or row (for vertical blocks), makes sure that they address the top left corner of the proper cell.
4. BlockMap provides the PositionOnBoard value to plug into the Block record for a dropped block.  The SolutionIndex was filled in for each block when the case was defined so it becomes a simple matter to run through the block and check if all are in the correct location.  If they are, give the user a "Congratulations" message.
5. When the Hint button is clicked, we want to either remove one  block that is in on the board but in the wrong location  or move a random unplaced block to the correct location on the board.  BlockMap will tell us where the correct location is.  (For block N, scan Blockmap looking for the cell entry containing data [N,0]. 

Another slightly tricky bit is converting clicked pixel positions to cell locations.  The TStringGrid MousetoCell method does this for us.   When we drop a block on the board, we also use the Cellrect method to determine exact pixel values on which to drop the block.

There's probably some other stuff that needs describing, but it's getting late. As usual, use the feedback link to ask if you have questions or suggestions.

 Running/Exploring the Program 

Suggestions for Further Explorations

  [Feedback]   [Newsletters (subscribe/view)] [About me]

Copyright © 2000-2018, Gary Darby    All rights reserved.