
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
Here's a program illustrating an efficient
way to exactly cover a given rectangle reasonable shaped rectangles.
Background & Techniques
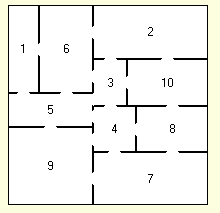
"Robot Rooms" implements an algorithm for exactly
covering a rectangular area with random rectangles meeting certain size and
shape constraints. The authors' 2001 paper "Data Set
Generation for Rectangular Placement Problems", C. L. Valenzuela and P. Y.
Wang, is available at
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.39.3218
The paper slightly complex but well presented and requires no
more than high school math and a few hours of study to digest. It proves the
existence of exact rectangle coverings with rectangles that are constrained
by aspect ratio (are not too long and narrow) and by area ratio (restricts
range in size). The proofs provide the basis for an included algorithm
for generating random coverings.
It was just what a long time DFF viewer needed generate a random arrangement of
rectangles (rooms) for a Delphi investigation of intelligent robot behavior.
I helped him by providing a way to create "doorways" connecting adjacent
rooms. I found the problem so interesting that I independently implemented
the "room generator" algorithm as well.
The program allows user control of base size, aspect and area ratios, and number of
rooms to create. Two features used for debugging were retained : 1.)
an option to display text for generated rectangles and 2.) the random seed
used to generate each set of rooms. This can be useful for generating the
same set of rooms multiple times.
Notes for programmers
The paper referenced above proceeds step by step proving several theorems
working up to:
1. Theorems 1 through 4: Given an aspect ratio, ρ
(Greek letter Rho), representing
H/W of a rectangle, and a starting rectangle whose aspect ratio is between
1/ρ and ρ,
it is possible to subdivide the starting rectangle into an arbitrary number
of smaller rectangles, each of which meet the same aspect ratio criteria.
2.Theorem 5: Given an area ratio. ϒ
(Greek letter Upsilon), representing largest area divided by smallest area of a set of rectangles, it is possible
to subdivide any starting rectangle into an arbitrary number of
smaller rectangles, each set of which meet the area ratio criteria.
3. Theorem 6: Theorems 1 through 5 can apply to a starting rectangle meeting the
aspect ration initial condition. This allows arbitrary subdivision into as
many rectangles as desired, each meeting both Rho and Upsilon conditions and
cumulatively exactly covering the original rectangle.
The algorithm for implementing Theorem 6 :
 | How to choose the rectangle to split next which will maintain the
area ratio condition , |
 | The direction (or directions) in which to divide the rectangle
(horizontally or vertically), and the range of offsets from the
top or left end of an edge which will maintain both the aspect and area
ratio conditions.. |
Although the procedure described is recursive in nature, (each rectangle
has the same steps applied) it seemed natural to implement the solution as a
loop:
 | While more rectangles are needed
 | Select a rectangle to split
 | Get area, m, of largest
rectangle |
 | Make a list of rectangles whose
area is > 2m/ρ |
 | Randomly select one. |
|
 | Split it.
 | If selected rectangle can be
split either Horizontally or Vertically, randomly choose one.
Otherwise just use the only valid direction. |
 | For split direction chosen,
calculate the valid range of offsets. |
 | Select random split point within
this range to define a new right or bottom edge. |
 | Replace existing rectangle
definition with left or top rectangle and create a new
rectangle defining the right or bottom portion the split.
|
|
|
 | End |
Everything else, as they say, is details.
The "door generator" portion of the
program makes vertical doorways by sorting the rectangles by increasing left edge X
offsets within top edge Y offsets and then checks top and bottom edge lines
with the following rectangles looking
for vertical edges which are co-linear and overlap. Given two colinear
edges, function Overlap returns offsets of the overlapping portion. These overlap
line segments are candidates
for receiving a doorway if they are wider than the specified door width.
The same process, sorting by increasing Y coordinates within left edge offsets will find
candidates for horizontal doors.
Running/Exploring the Program
Suggestions for Further Explorations
|
Original Date: January 10, 2012 |
Modified:
May 15, 2018 |
|
| |
|

