Problem Description
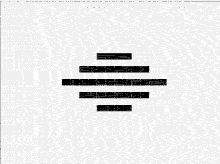 |
 |
 |
| 4_8_12_Diamond
(Start) |
Generation 10 |
Generation 46 (last) |
Here are two versions of the "game" of Life, an
example of cell automata; things (cells) that can reproduce and die
based on their environment.
Background & Techniques
Every puzzle and game programmer's portfolio should include two
standards, John Conway's Game of Life and Fractals, neither one of which
currently appears here on DFF. Today's posting will fill one of those
gaps. I decided to do it while searching for a beginner's level
program since I have been neglecting them recently.
The problem is, I now serve two masters - programmers interested in the code
and real people who are interested in running the code for some
entertainment, educational, or practical purpose. And most
beginner level programs are not likely to be very interesting to users. So
here are two versions; one as simple as possible for the beginning Delphian
and one that that builds on the simple version.
Mathematician John Conway designed the game in 1970 based on two simple
rules. The board is a rectangular grid of cells each of which is
either occupied or empty. After setting an initial starting set
of occupied cells, we move to the next generation according to rules about the
the state of the neighbors, the 8 cells which surround it.
Rule 1: If an occupied cell has two or three neighbors, it is happy
and remains unchanged. Otherwise it is too lonely or too crowded and
dies (cell becomes unoccupied).
Rule 2: If an empty cell has exactly 3 neighbors, a birth occurs
and the cell becomes occupied. Don't ask me what kind of life form
requires three parents for a birth - I didn't make the rules!
That's it. Search the web for Conway's Life and you'll find many,
many
pages of sample patterns, an entire lexicography of named terms for patterns
and behaviors, and a number of other programs including one written in
Delphi which handles board sizes up to 1 million x 1 million cells!
And lots of discussions of gliders, sliders, boats, guns, spaceships and
oscillators just to name a few.
The simple version, V1, changes the state of each cell that
gets a mouse click for setting up a pattern. The Step button creates the next generation.
The board is 25x25 cells. That's about it.
Version 2 adds the ability to load and save pattern files,
automatically moves from generation to generation at a user specified rate,
and allows board to be set to 25x25, 50x50, or 100x100 cells.
I have included a few sample pattern files as a starter set.
You can find hundreds more at
http://www.argentum.freeserve.co.uk/lex.htm. Simply copy and
paste a pattern into a text file to load and run it. The files
are the simplest possible format, a text file array of '.' and 'O' characters define
the pattern ('O' = 'Occupied'). The array is centered on am empty grid
when loaded into the program.
For either version, patterns that expand beyond the limits of the
grid "wrap around" as if the first column was to the right of the last
column and the top row was below the bottom row. Topologically its as
if the board was printed on a cylinder whose ends were then joined together
to make doughnut (Ok, a torus, if you want to be technical)..
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
executable version of Version 2 of the program.
Notes for Programmers
Version 1 uses two 2-dimensional arrays of Boolean (true/false)
variables, CurrentGrid
and NextGrid, to hold the
current and the next generation configurations, (True for occupied, False
for empty). The new generation depends on
the old generation neighbor counts before any updating occurs, thus the need
for two grids. A TStringrid control, Stringgrid1, provides the visual
picture of the current configuration. The
MakeStep procedure generates each new generation by counting the
neighbors for each cell and applying the rules described above to set the
cell value in NextGrid and StringGrid1. After all cells
have been checked, NextGrid is copied to CurrentGrid.
MakeStep contains about half of the 100 user
written instructions in the program. The other routines are event
exits which are called automatically when certain events occur:
 | Board size can now be changed by the user.
This means that the arrays must now be dynamic. I combined
CurrentGrid and NextGrid into a single Grid array with
a 3rd dimension. Grid[0] and Grid[1] now
contain current and next generations with their roles determined by
variables Active and Next. Before updating, Next
is set to (Active +1) mod 2 which effectively points it to the
non-active array. After it is updated, Active is set to
Next. |
 | The StartBtnClick routine, which
just called MakeStep in V1, now contains a
new loop making new generations at a rate selected by the user.
MakeStep is now a function which returns true if the new
generation changed from the old. This allows the loop to know when
to stop. Note that lots of patterns end in oscillators which the
current code does not recognize. |
 | The radio button group control
RateGrp allows the user to select from several refresh rates as next
generations are created. The OnClick exit for
RateGrp, RateGrpClick, sets a global LoopTime variable
which StartBtnClick uses to sleep awhile between generation
updates. |
 | Procedure Setsize resets to program to
an initialized state. It is called from a number of other
event routines
 | SizegrpClick when grid size is
changed. |
 | RestoreGrid called from a new RestoreBtn button to reset the
board to its initial pattern state. |
 | FormActivate to initialize at
program start time. |
 | :LoadBtnClick before loading a new
pattern |
 | ClearBtnClick to let the user clear
a pattern and reset counters. |
|
 | .FormResize is called when form
size is changed. StringGrid1 has its anchor properties set
to left, right, top and bottom so the grid expands and contracts
automatically when the user resizes the form. FormResize
resets the row height and column width to fill the new size as nearly as
possible.
|
 | Load and Save buttons. LoadbtnClick
loads a file and calls the Savegrid procedure to make a copy of
the initial pattern which can be restored later using RestoreBtn. |

