
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
A recent email:
"Hi I have been searching the
internet for a trick using square cards (or paper) with
numbers and holes in them. The trick was to choose any
number on the cards and one at a time turn each card to "yes" or
"no" written on each card depending what cards have that
number. after that the pile is to be turned over and the
chosen number is shown through a hole on the bottom of pile.
Do you know How I might search the internet for this?
Any help would be
appreciated.
Thanks, Peter
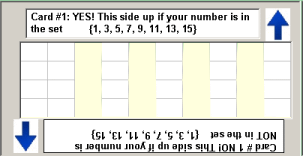
Background & Techniques
It seemed clear that this was a binary coding trick. I
decided to implement a sample set but with some modifications.
The final card of the deck described by Peter probably had all of
the numbers on it with the word "YES" and the numbers printed
again on the back of the card in specific positions. This
card would always be the last card placed on the stack of "YES"
cards and therefore , when turned over, be on the bottom with the
numbers on it's back side showing through anywhere there was a
hole in that location on every card. My card
with all of the numbers on it will lie face up and have the
Yes/No cards laid on top of it.
Peter couldn't remember where the words "YES" and "NO"
were written or what type of rotation was required.
But the idea will be to align N cards (for numbers in the range
0 to 2N-1) and with the holes in each representing the 0 and
1 bits for a specific bit position for the numbers printed on that
card.
I chose to use the top half of the rows on each card for the
"0" bits and the bottom half for the '1" bits. Rotating the
"No" cards by 180° will then move the "0" bits to the bottom half
to line up with the "1" bits in the same position on the "Yes"
cards. (Note that if we fill in the "1" bits in increasing numeric
order, the "0" bit rows must be reversed since rotating will
reverse them again.)
As a simple case, assume we are implementing the trick
for numbers {0,1,2,3}, 2^2. In binary {00, 01, 10, 11} so our cards could look like this:
|
Base card |
| |
|
|
|
| 0 |
1 |
2 |
3 |
|
Base card |
Now we need a card for each bit position, in this 0 to 3
case, the right bit (1's position) card and the left bit (2's
position) card and. From the way the the numbers are laid
out the base card, we can determine which squares must be cut out and
which must be left closed for each row and column on each card.
Label the cards with the numbers which have that card's bit position
turned on in their binary representation. Then cut out the squares
in the bottom row which will line up with those numbers as printed on
the base card. Now rotate the card 180 degrees so that the "NO"
side is up and cut out all of squares in the new bottom row except those
which would let any of the numbers n this card show through.
Not a very clear explanation I'm afraid, but I can't seem to figure out
how to say it better. Here's what the cards would look like:
Left bit card▲
Right bit
card▲
The top row with 4 cells represents
the "0" bits in the binary representation of the 4 numbers , but
since we will invert the cards that have a 0 in that position,
we must fill in the holes in reverse order (inverting will put
them back in the correct order). The 2nd row with 4
cells has holes for the numbers with "1".
And we could, of course, label the
base card with symbols {1 2 3 4} or (A B C D} or {chicken, cow,
horse dog} or any symbols we choose so long as the Yes/No cards
are labeled appropriately.
The sample program which can be downloaded below expands
this idea to numbers 0 to 15 by including 4 rows with holes, two
rows for "0" bits and two for "1" bits just to keep the cards
from getting too long.
In operation, I included arrow
symbols which rotate the cards to bring the No message to the
top. Click and drag on the grid will let you drag
the cards to the Base Card position to see the results.
A "Reset" button moves the
cards back to their original configuration. A "Print"
button prints the form for anyone who wants to make a
physical set to prove to themselves that the program (hopefully)
works.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
executable version of the program.
Notes for programmers
A good programming exercise here with several complications.
 | I thought the message at the bottom of the card should be
inverted so that involved resurrecting the U_Invertedtext unit
from our
InvertedText demo program. |
 | Dragging is still more complex than it seems it should be,
but the cookbook approach from
Drag Image demo passed the test pretty well. The
complication was that we want to drag a card (Tpanel)
which contains other controls (TStringgrid, TMemo,
and Timage ), and we wanted start the drag with a click
anywhere on the card including those controls. |
 | I never could get the OnClick event for the arrows
and the OnStartDrag event to coexist, so I still don't
understand all I know about that subject. For now, the
arrows are excluded from starting the drag operation. If
anyone knows how to handle this, let me know.
|
 | It took more than a little fiddling to get the correct row
and column assignments for the "0" bit rows. |
Programming is so humbling! If you ever get to feeling
quite smart, just try a program that has to emulate some task
that is simple and natural for the human brain (like turning a
cord over or placing it on a stack).
Addendum December 19, 2007: An update was posted to day to
improve the visual layout of the the cards.

Running/Exploring the Program
Suggestions for Further Explorations
 |
Larger version with 32 numbers (5 Yes/No cards) or 64
numbers (6 Yes/No cards). |
 |
Resolve conflict between click processing for an image with
n OnStartDrag exit. |
| Original Date: July 6,
2006 |
Modified:
May 15, 2018
|
|
|

