What's New -  March, 2016

[Home]

March 3, 2016:  Graph searching is a powerful tool for solving problems which move from state to state as it is solved.  Think of a graph as a bunch of nodes (points) connected by edges (lines). These might  be cities connected by roads or  house connected by water lines, etc. where finding shortest paths might have real value.   Most board games and puzzles are can also be represented by graphs where nodes are board states and edges are the moves that get from one board state to the next.  For example, the February 20 "Coal to Diamonds" puzzle below can be the initial node with nine edges running to the 9 boards (nodes) resulting from clicking on each of the 9 squares.  Each of those in turn will have up to 9 new edges as the next possible moves, etc.  Eventually, there will be an all diamonds board (the solution) and the search objective is to find the shortest path from node to node which connects the initial board with the goal board.

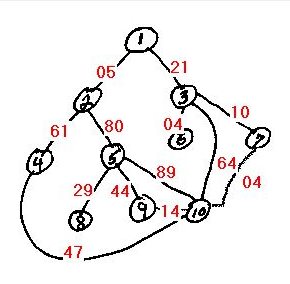
Shortest 2 to 10 path: 2-1-3-7-10

The original demo illustrating the Dijkstra algorithm (method) for finding shortest paths, calculated the shortest path from Node 1 to node 10 of a sample graph using random weights (distances) from node to node.  The search was one-way (i.e. could only move to higher numbered nodes), but a programmer recently modified the program to search from node 2 to node 10.  A problem surfaced when the shortest path happened to be 2-1-3-7-10 which required traveling backwards through node 1.  Shortest Path Demo Version 2.0 posted today incorporates two-way searching and allows users to specify both the start node and the goal node.  
         

An intermediate level exercise posted in our Delphi_Techniques code section based on a a user's request for help drawing doors subdivided with  one or more vertical frames separated and divided by mullions of a given width and position.   Find out more and download source and executable file at DrawingDoorFrames. 
 

March 25, 2016:   I first posted a program to calculate the distance between two points on the earth's surface in 2004.  Distance is understood to be the shortest distance which is slightly mind-blowing when  the Great Circle Route says that if you fly from New York to London,  you must fly north over Newfoundland first !  Except at the equator, the shortest path to a location directly East of you involves starting out in a Northerly  or Southerly (Southern hemisphere) direction and arrive traveling slightly South (or North). 

Latitude Longiitude Distance Version 3.0 posted today is in response to a request from a blind(!) Delphi programmer working on a program that will allow other blind people to follow Great Circle routes from point to point and "explore" where they travel along the way.    To do this Stefan needed a way to plot the bearings at steps along route.  Version 3.0  does that by displaying points traversed when moving from given a starting bearing and a total distance.  User can select 1, 10, or 100 steps and see the coordinates and the new bearings at each step along the way.   I wish him the best in adapting this code to his application.

In the process, I uncovered an occasional "final bearing" error in my previous implementation of the  algorithm which finds points from distances.  I made, and now use, a conversion of a National Geographic Information System  (NGIS) Fortran program which is not only simpler, but eliminates the error.