
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
Numbrix™ is a puzzle currently (September, 2008)
being published in the "Ask Marilyn" column of the weekly Parade Magazine
and daily in the "Fun and Games" section of the
Parade Magazine website.
The puzzle board is a square array of cells, 7x7,
8x8, or 9x9 in puzzles seen so far. For a puzzle with N cells per
side, the objective is to fill the cells with integers from 1 to NxN contiguously with
each number after the first adjoining the next lower number vertically or
horizontally. Some of the numbers are pre-filled and the user's
additions must interface with those to keep the entire number chain in
proper order.
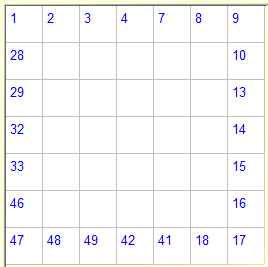 |
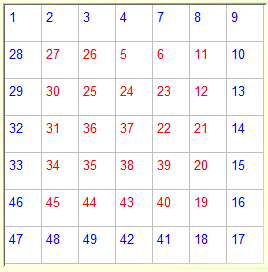 |
|
A Numbrix Puzzle |
Solved! |
Background & Techniques
The puzzles are satisfyingly solvable, some would say "too easy"
but I enjoy them more than Sudoku. Several sample puzzles are included
in the program which may be accessed with the Load button
You can solve the puzzle yourself by entering numbers
in available squares (any that are not prefilled). The Check button will verify any trial solution. If you want some help,
the Fill forced locations button will fill in
all numbers which have only one valid location based
the geometry of pre-filled values. Each click will make
one pass through the board filling additional numbers if
possible.
The Solve button does a depth-first search search for a
solution, backtracking for each dead-end path it tries.
Solve time is displayed in seconds or milliseconds so
you can observe the effect of pre-filling the forced
locations on solution times if desired.
Controls used for debugging were left in place for future
changes/fixes but are normally invisible. The Show debug controls
checkbox will make them available. Users may drag the Show progress
control bar to any slower position to watch the
search process.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
an
executable version of the program.
Notes for programmers
The solution search was the most satisfying part of this project.
FindNext is the recursive function which performs a depth first
search. Because we are progressing from low to high numbers, we we
don't have to worry about looping, i.e. repeating a position that we have
already visited. The pseudo code for puzzle size N looks like
this:
Findnext(fromcell, fromvalue):boolean
 | Result=false; |
 | Insert Fromvalue into Fromcell |
 | If Fromvalue is the last point (NxN) then set
result=true and exit. |
 | Fromvalue not the last point:
 | Set Nextvalue=Fromvalue+1,
|
 | For each of the 4 directions check
the neighbor (Nextcell)
 | Is Nextcell empty and Nextvalue
not predefined?
 | Yes: Result=Findnext(.Nextpoint,
Nextvalue) |
 | No: If Nextcell already
contains Nextval then this is a predefined number,
 | Result=Findnext(Nextcell,Nextval); |
|
|
|
 | end neighbor search loop |
|
 | if Result=False and Fromvalue was not
predefined then set Fromcell abck to empty |
Procedure SolveBtnClick makes the initial call to
FindNext passing the location, or a possible location for the first
entry ( "1"). Location is a one dimensional array
containing NxN the cell coordinates for all predefined numbers or
(0,0) if not predefined. Findnext uses Location to
checked for predefined numbers. It is also the used to build a list of
cell locations where 1 might belong if it is not predefined. The
solution can start at any cell that is within the lowest predefined number
of cells from its location. For example, if the lowest predefined
number is 5 and is located at (1,1), then 1 must belong to any empty cell
within the rectangle defined by (1,1) to (5,5).
SolveBtnClick builds a list of these cells and make the initial call
with each of these possible starting points until a true result is found.
The other interesting aspect of the code was setting up the controls used
to bug the search code. It is helpful to watch the search proceed if
one can watch the point where the error exists. Unfortunately that may
be several thousand moves into the search and could take hours reach.
By setting limits for the display animation and forcing a pause when a
specific number is reached, the error location can be located quickly (or at
least a lot faster than without the controls :>). A
trackbar controls the pause time after each changed board is displayed.
Setting the bar to its max position by passes the animation completely.
When the specified value is placed in a specified cell, a pause loop is
entered allowing the programmer to set a break in code or to change the
pause values before continuing. This is accomplished by setting
a "Pause" flag to true and looping with "Sleep" and "application.processmessages"
commands until Pause=false. Clicking the displayed pause
message sets Pause to false.
Addendum October 9, 2008: A Numbrix puzzle generator was
posted today. It generates puzzles of several sizes and has a few
options. Users may choose to define the border cells as the
predefined values or may click cells to define any other pattern.
Puzzles up to 10x10 cells in size may be generated. A small change to
the Numbrix program allows it to solve 10x10 puzzles also.
Running/Exploring the Program
Suggestions for Further Explorations
Done October 8, 2008: A "generator" would be a nice addition
to the program. Simply generating a random starting point and a random
direction for each successive number would usually not succeed because
unreachable holes would be left and stop the generation before the puzzle
was complete. So we would need to generate random moves with the
constraint that each number added must not leave unreachable cells or "one
way streets". Twisty alleyways that are two cells wide, so numbers
could be added down and back would seem to make a harder puzzle than those
that are continuously filled as we progress.
|
Original Date: September 28, 2008 |
Modified:
May 15, 2018 |
|
|
|
|

