Here are two problems (#16 and #17), adapted from the book
Fifty Challenging Problems in Probability  Frederick Mosteller, Dover
Publications.
Frederick Mosteller, Dover
Publications.
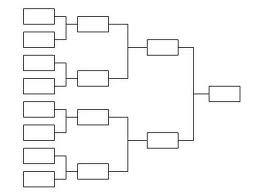
Problem 16:
Eight tennis players (call them A,B,C,D,E,G,F,H) are randomly assigned to
start positions in a ladder tournament. Initially, position 1 plays position
2, position 3 plays 4, 5 plays 6 and 7 plays 8. Second round has 2 matches:
winner of (1,2) match plays winner of (3,4), and winner (5,6) plays
winner(7,8). The winners of the two 2nd round matches play each other in the
final match. Player A wins against any of the others. Player B always
beats any opponent except player A. What is the probability that player B
wins the 2nd place trophy in the final match?
Problem 17: In the same tournament type as in the previous problem, assume that the
8 players are of equal skill levels so
each has a 50-50 chance of winning any particular match. A and B happen to
be twins. What is the probability that they will play each other in some
match during the tournament?
I enjoy working on probability theory problems even though it's
not my strongest subject. The problems tend to be easy to state and
understand, but sometimes irritatingly difficult to solve. The
"Fifty Challenging Problems" book has a number that are interesting, of which the
two are presented here. The problems in the book have
solutions provided, but I only use them as the last resort. Over the years I have developed the habit of
experimentally finding or verifying solutions to probability problems.
Modeling the problem in code is fun and confirms that the problem was
understood. The results of running a million trials takes only a
second or two and, if both are done correctly, ensures that
experimental and analytical results will closely agree.
I've used that approach here and the program presents both my analytical solutions
developed without reference to solutions in the book and the experimental results. l promised
myself to refer to the book solution only if my analytical and
experimental result did not agree. In this case they did, but that
leaves 48 mores opportunities to fail and learn.
I plan to augment this program with additional problems in
the future so having this page as a base will help get over the documentation
hurdle when I do.
Addendum February 7, 2012: Here are two more
problems which I fond interesting and added today in Version 4:
Problem 18: If 100 coins are
tossed, what is the probability that exactly 50 heads will be showing.?
Problem 19: Samuel Pepys wrote
Isaac Newton to ask which of these events is more likely: that a person get
(a) at least 1 six when 6 dice are rolled. (b) at least 2 sixes when 12 dice
are rolled, or (c) at least 3
sixes when 18 dice are rolled. What is the answer?
February 27, 2012: Version 5.- adds one more
problem:
Problem 20: A, B, and C are to
fight a three cornered pistol duel. All know that A's chance of hitting his
target is 0.3, C's is 0.5 and B never misses. They are to fire at their
choice of target in
succession in order A, B, C, cyclically (but a hit man is out of the
contest, neither shooter
nor shot at), until only one man remains. What should A's strategy be?
The analytical solution for this one involvesl geometric
progressions because the chance that you will win at round N+1 is the chance
that you had of winning at round N times the chance that both you and your
opponent miss on your next turns (otherwise the match is over and there is
no round N+1). By definition, a sequence where each term is a constant
multiple of the previous term is a "geometric
sequence". It took a long time to find the correct
analytical solution because there are lots of chances for arithmetic
errors in determining the initial value and the ratio for the
sequences. Fortunately, once the appropriate initial value, a,
and ratio, r, have been determined, the overall probability of
winning for each contestant is the sum of the probabilities of the
individual outcome which is a/(1-r).
Running/Exploring the Program

