Problem Description
Here's a little program that estimates the
surface distance between two points on earth defined by their latitude and
longitude.
Background & Techniques
A viewer recently requested this facility which happened to pique my
curiosity. A usual, there is lots to learn but the basic concepts
are not too difficult.
Latitude and Longitude represent the angle portion of a point in space
defined in polar coordinates. Recall that in 2 dimensional space a
point may be defined either by Cartesian or polar coordinates. A
Cartesian coordinate defines a location as the horizontal and vertical
distance from some fixed point, the origin. Polar coordinates define
a point by the length and angle of a line segment from the origin to the
point. There is a Math-Topics page illustrating the relationship
between the two systems. Now, if we imagine a point on a flat
2-dimensional page defined by the two numbers and then we want to move the
point into 3-dimensional space by lifting up off the page, we need one
more number. For Cartesian coordinates, the third number will
be the height of the point above the page. For polar coordinates,
we'll rotate the line segment up off of the page and measure the vertical
angle from the page up to the line.
Latitude and Longitude are the two polar coordinate angles.
If we imagine ourselves at the earth's center with the top our head pointing to
the North pole and out feet toward the South pole, the equator will be at 90 degrees from North - straight
out in front of us. . This imaginary line around the earth at
a 90 degree angle to the North pole is defined as 0 reference for
measuring Latitude, the North-South angular coordinate of a
point. Another imaginary line running north and south along the
surface of the earth and passing through the
poles and Greenwich England is the 0 degree reference for measuring
East-West angles, the Longitude. Latitudes range from 90 degrees
North to 90 degrees South with South angles treated as negative.
Longitudes range from 0 to 180 degrees East and West with West angles
treated a negative.
The actual math to calculate the distance between two points is
straightforward and derived in many places on the web, namely:
angular distance = arccos(Sin(lat1) * Sin(lat2) + Cos(lat1) *
Cos(lat2) * Cos(lon1-lon2)) and assuming that the angle is given in
degrees, distance = distance per degree*angular distance =
(2*Pi*radius/360)*angular distance. This is the spherical distance estimate produced by this program.
Flat Earth?
The above explanation considers the third parameter of the polar
coordinate defining a point, the length of the line segment, to be
constant, namely the radius of the earth. But in fact the earth is
not spherical. Our rotation has caused the earth to bulge slightly at
the equator and flatten at the poles. Sir Isaac Newton
in the 1600's calculated the radius at the poles to be 0.9967 of the
radius at the equator. The current value is about 0.9966 so
Sir Isaac didn't do too badly. The difference of the two
circumferences (polar and equatorial) is about 83 miles, so spherical
coordinates for two points on on the equator but 180 degrees apart should
produce the maximum error, about 40 miles. By the way,
these distance estimates are "great circle estimates" meaning
they lie on the path defined by the plane through the two points plus the
earth's center and the surface of the earth. The great circle
route is the shortest surface distance between the two points.
Counter-intuitively, if you are north of the equator and want to get to a
point directly east of your current location, don't head east - the
shortest way is to start out traveling northeast and arrive traveling
southeast!
Calculating distances taking into account the elliptical shape of the
earth is quite complex. There are approximations that are at least close
to the true distance as those that assume a spherical earth.
The one used here is from http://www.codeguru.com/Cpp/Cpp/algorithms/general/article.php/c5115/
Addendum October 3, 2008: After 4 years, it must be
time for an update. A viewer wrote recently asking how
to calculate an end point given a starting point, a bearing, and a
distance. After some searching, I found Vincenty's algorithm and
equations. In 1975, geodesist Thaddeus Vincenty published
equations that produced very accurate results by iterating intermediate
results. It was one of the early applications to geodesic
measurements during the period when applications were moving from
desktop calculators to computers. Versions for both the "distance
between points" problems and the "endpoint from start, bearing and
distance" problem. Both are included in Version 2 of LatLong
Distance program posted today.
March 25, 2016: Time for the next edition. This time in
response to a request from a blind(!) Delphi programmer working on a program
that would allow "blinds" (his term, so I guess it's OK) to virtually travel the
earth by moving from one Lat-Lon point fin a direction for a distance. We both learned that things get tricky if "distance"
means "shortest distance" as it does in this program. If I pick a point Northern
hemisphere and stretch a string to another point straight East at
the same latitude on a globe, you will see that you must start travelling slightly
North of East to get there. This is the
"Great Circle" effect. I had developed code to plot points code along a
constant bearing, but after thinking about it, Stefan decided he like traveling the
Great Circle route. He did need a way to plot the bearings at fixed
distances along the
way. Version 3.0 posted today does that displaying points travel along the
great circle from a point given a starting bearing and a total distance.
User can select 1, 10, or 100 steps and see the coordinates and the new bearing
at each step along the way.
In the process, I discovered a coding error in my previous implementation of
the Vincenty direct algorithm which caused bearings to be off by 180° under some
conditions. After several days of looking for my error, I made (and now
use) my conversion of an NGS (National Geographic Information System) Fortran
program which is not only simpler, but eliminates this error.
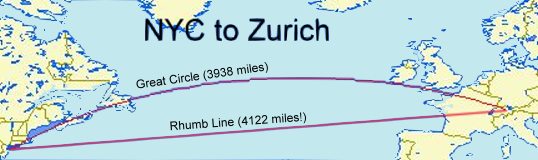
April 15, 2016: One more feature was added today.
When calculating an end point from a start point, direction and distance,
Version 3.2 allows the user to choose between Great Circle and
Rhumb
Line travel . Great Circle travel is the shortest route between two
points because it follows intersection of the earths surface with the plane
formed by the start point, the destination and the center of the earth.
The disadvantage is the travel requires continuously adjusting the direction of travel
as measured by the "latitude/longitude" measurement system,. The
new Rhumb Line option allows one to travel at a constant bearing from where you
are to where you want go or to explore what lies at a a given direction at a given
distance. But, unless you tunnel, every inch traveled that is not on the
Great Circle route takes you further from the center of the earth and therefore
increases the distance traveled to the destination. Constant bearing (Rhumb line) travel is not
the shortest way to get there, just the simplest.
June 3, 2017: With multiple programs using our LatLonDistance
unit, it has been relocated to the DFF Library unit (DFFLibV15).
This program now exists in the Library section of the site and references the
LatLonDistance unit in its new location. The
routines in the the unit and this test program have both been converted to
accept and return Latitude, Longitude, and Azimuth (Bearing) values
in degrees instead of radians. The actual calculations require radians,
but the necessary conversions for inputs and outputs are now handled within the
routines and should be transparent to the calling programs.
Running/Exploring the Program

