
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
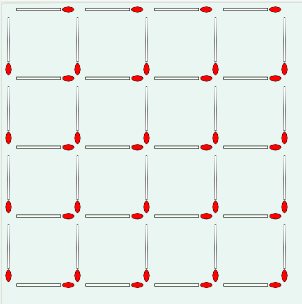
There are 30 squares of all sizes in a 4x4 grid of 40 matchsticks. "What is
the minimum number of matchsticks that need to be removed to leave no
squares of any size?"
Background & Techniques
Here's an investigation from the latest addition to my library of math &
puzzle books: Challenging Math Problems,
Terry Stickels, Dover Publications, 2015,
Problem #12 in the book shows 24 matchsticks formed into a 3x3 grid and asks
about the fewest sticks that can be removed to eliminate all complete squares of
any size. Actually one solution is given and the real question is
"What is the minimum number of matchsticks that need to be removed to
leave no squares of any size?". This program will not tell you directly,
but will let you play around by adding and removing sticks from the grid with
feedback at each step about the number of squares remaining.
As regular viewers know, mathematics is among my interests thus I decided to
look into the properties of integer sequences formed by increasing grid sizes.
An excellent resource for this is the
Online Encyclopedia of
Integer Sequences. I tracked Number of matchsticks, Number of
squares of all sizes, and Minimum
# of matchsticks removed for a zero square solution. It's easy to get values
for 1x1, 2x2, and 3x3 grids and the program will provide values for the
Matchstick and Square counts for larger sizes. Surprisingly, all
three sequences exist and have names in the OEIS library. A search on the first
few terms will find them with an large amount of additional detail.
Check it out and have fun!
Non-programmers are welcome to read on, but may want to jump to bottom of
this page to download the executable program now.
Programmer's Notes:
There were several interesting problems to solve in coding this program:
 | Data Structure was tough design because most of the referencing is the
edges of the grid but most of them share a vertex one, two or three other
"matchsticks". I ended up with an array (Vertices) of
TVertext records representing top left corner of a cell.
Each TVertext record contains two TEdge records, labeled
H for horizontal and V for vertical direction. Each
TEdge record has a TLine record with the start and end
coordinates of the matchstick, a direction field (East or South),
and a Boolean Exists flag to tell whether the stick is present.
The rightmost H record and the bottommost V record have
direction set to Unknown to prevent checking nonexistent edges.
|
 | Detecting matchstick clicks uses the MouseDown event exit
which scans all edges using the NearestEdge function to return the
intended edge. A simple Exists:= not Exists;
statement then reverses the edge state and a call to DrawEdge
redisplays it. |
 | Drawing matchsticks instead of just red or gray lines was a late
addition and required lots of time to get the scaling even close to
correct over multiple grid sizes. A Cellsize value
is calculated based on image size and specified number of grid rows and
columns. The length of each matchstick is based on Cellsize
value, allowing a little space at each end of the stick. Matchstick
width (MsW, match head width (MhW,) and match head length (MhL)
are all trial and error values based on cell size. Each match is drawn
as a red ellipse for the head and a rectangle for the stick, overlapping the
head slightly. |
 | Counting and reporting matchsticks removed is trivial; check edges
in all vertices and count those with Exists=False. Counting all
remaining squares was not so simple. A IsSquare function checks
the perimeter of each passed top left vertex and size from current column
and row to the right and bottom edges If any is missing a matchstick, that
combination is not a square. |
 | For Version 2, it took a while to figure out the best way to view
remaining squares in larger grids. Highlighting matchstick was not
useful for large grids (with small matchsticks). Solution was to use
the TCanvas Copyrect method to save the grid image to a bitmap before
highlighting a square whith a solde rectangle and then restoring from the
bitmap after a 1.5 second delay. |
 | Save and Restore were implemented as dialog units which save and restore
grid configurations in configuration file HowManySquares.ini.
Grid names are used as Section names, Two digit strings contain
vertex column and row as Key names, and two character Value
strings: __, H_, _V, and HV.
to identify presence or absence of matchsticks from that corner. It
works fine and saves creating a file for each grid saved. |
January 28, 2016: It did not take long to recognize the need for
for the first two enhancement suggestions. Version 2.0 adds the ability to
view remaining squares after each move or on request. Also grids can now be
saved and restored in configuration file "HowManySquares.ini" Both features are
helpful when working on larger
grids.
Incidentally, I didn't get to documented it within the program, but the
optimal solution for an N x N grid removes N*(N+1)/2
matchsticks.
May 19, 2018: It finally happened - someone found a better
solution for the 4x4 grid than my program thought possible.
Version 2 posted today has a revised "best" solution target formula: For
an NxN grid, best solution removes
Ceiling(N*(N+1/2))/2) matchsticks where Ceiling(X) is the smallest integer
greater than or equal to X. SO the new best solytion for the 4x4 grid is
Ceiling(4*(4.5)/2)=18/2=9 instead of the old target of 10. If you can't
find it, for a $2 donation, I'll send you the 9 toothpick solution and split it
with the fellow that sent it to me. I'm so confident of the new targets
that I'll donate $10 to the first person to send me a 5x5 solution
less than 14 toothpicks, or a 6x6 grid solution less than 20.
Running/Exploring the Program
Suggestions for Further Explorations
 |
Implemented Jan 28,2016: Add ability to show remaining squares. Count
of squares is currently displayed but finding them is not always easy.
|
 |
Implemented Jan 28,2016: Add ability to save and restore grid
configurations. |
 |
Check non-square grids. The capability
exists but has not yet tested. |
| Original: January 19, 2016 |
Modified:
May 19, 2018
|
|

